RESISTENCIA ELECTRONICA

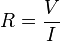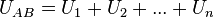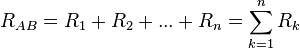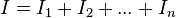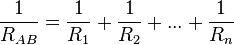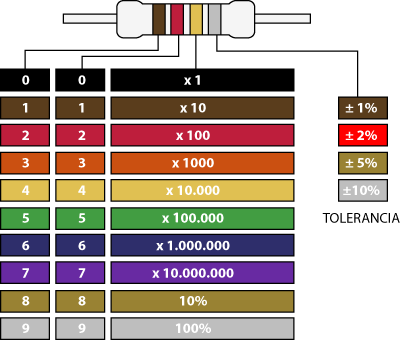
Se le denomina resistencia eléctrica a la igualdad de oposición que tienen los electrones al moverse a través de un conductor. La unidad de resistencia en el Sistema Internacional es el ohmio, que se representa con la letra griega omega (Ω), en honor al físico alemánGeorg Ohm, quien descubrió el principio que ahora lleva su nombre.

Para un conductor de tipo cable, la resistencia está dada por la siguiente fórmula:

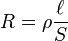
Donde ρ es el coeficiente de proporcionalidad o la resistividad del material,  es la longitud del cable y S el área de la sección transversal del mismo.

La resistencia de un material depende directamente de dicho coeficiente, además es directamente proporcional a su longitud (aumenta conforme es mayor su longitud) y es inversamente proporcional a su sección transversal (disminuye conforme aumenta su grosor o sección transversal).

Descubierta por Georg Ohm en 1827, la resistencia eléctrica tiene un parecido conceptual con la fricción en la física mecánica. La unidad de la resistencia en el Sistema Internacional de Unidades es el ohmio (Ω). Para su medición, en la práctica existen diversos métodos, entre los que se encuentra el uso de un ohmnímetro. Además, su cantidad recíproca es la conductancia, medida en Siemens.

Además, de acuerdo con la ley de Ohm la resistencia de un material puede definirse como la razón entre la diferencia de potencial eléctrico y la corriente en que atraviesa dicha resistencia, así:¹

Donde R es la resistencia en ohmios, V es la diferencia de potencial en voltios e I es la intensidad de corriente en amperios.

También puede decirse que "la intensidad de la corriente que pasa por un conductor es directamente proporcional a la diferencia de potencial e inversamente proporcional a su resistencia"

Según sea la magnitud de esta medida, los materiales se pueden clasificar en conductores, aislantes y semiconductor. Existen además ciertos materiales en los que, en determinadas condiciones de temperatura, aparece un fenómeno denominado superconductividad, en el que el valor de la resistencia es prácticamente nulo.

COMPORTAMIENTO CON CORRIENTE CONTINUA

Una resistencia real en corriente continua (CC) se comporta prácticamente de la misma forma que si fuera ideal, esto es, transformando la energía eléctrica en calor por efecto Joule. La ley de Ohm para corriente continua establece que:

donde R es la resistencia en ohmios, V es la diferencia de potencial en voltios e I es la intensidad de corriente en amperios.

COMPORTAMIENTO CON CORRIENTE ALTERNA

Figura 3. Diagramafasorial.

Como se ha comentado anteriormente, una resistencia real muestra un comportamiento diferente del que se observaría en una resistencia ideal si la intensidad que la atraviesa no es continua. En el caso de que la señal aplicada sea senoidal, corriente alterna (CA), a bajas frecuencias se observa que una resistencia real se comportará de forma muy similar a como lo haría en CC, siendo despreciables las diferencias. En altas frecuencias el comportamiento es diferente, aumentando en la medida en la que aumenta la frecuencia aplicada, lo que se explica fundamentalmente por los efectos inductivos que producen los materiales que conforman la resistencia real.

Por ejemplo, en una resistencia de carbón los efectos inductivos solo provienen de los propios terminales de conexión del dispositivo mientras que en una resistencia de tipo bobinado estos efectos se incrementan por el devanado de hilo resistivo alrededor del soporte cerámico, además de aparecer una cierta componente capacitiva si la frecuencia es especialmente elevada. En estos casos, para analizar los circuitos, la resistencia real se sustituye por una asociación serie formada por una resistencia ideal y por una bobina también ideal, aunque a veces también se les puede añadir un pequeño condensador ideal en paralelo con dicha asociación serie. En los conductores, además, aparecen otros efectos entre los que cabe destacar el efecto pelicular.

Asociación de resistencias

Resistencia equivalente[editar]

Asociación en serie[editar]Se denomina resistencia equivalente de una asociación respecto de dos puntos A y B, a aquella que conectada a la misma diferencia de potencial, U_AB, demanda la misma intensidad, I (ver figura 4). Esto significa que ante las mismas condiciones, la asociación y su resistencia equivalente disipan la misma potencia.

Dos o más resistencias se encuentran conectadas en serie cuando al aplicar al conjunto una diferencia de potencial, todas ellas son recorridas por la misma corriente.

Para determinar la resistencia equivalente de una asociación serie imaginaremos que ambas, figuras 4a) y 4c), están conectadas a la misma diferencia de potencial, U_AB. Si aplicamos la segunda ley de Kirchhoff a la asociación en serie tendremos:

Aplicando la ley de Ohm:

En la resistencia equivalente:

Finalmente, igualando ambas ecuaciones se obtiene que:

Y eliminando la intensidad:

Por lo tanto, la resistencia equivalente a n resistencias montadas en serie es igual a la sumatoria de dichas resistencias.

Asociación en paralelo

Dos o más resistencias se encuentran en paralelo cuando tienen dos terminales comunes de modo que al aplicar al conjunto una diferencia de potencial, U_AB, todas las resistencias tienen la misma caída de tensión, U_AB.

Para determinar la resistencia equivalente de una asociación en paralelo imaginaremos que ambas, figuras 4b) y 4c), están conectadas a la misma diferencia de potencial mencionada, U_AB, lo que originará una misma demanda de corriente eléctrica, I. Esta corriente se repartirá en la asociación por cada una de sus resistencias de acuerdo con la primera ley de Kirchhoff:

Aplicando la ley de Ohm:

En la resistencia equivalente se cumple:

Igualando ambas ecuaciones y eliminando la tensión U_AB:

De donde:

Asociación mixta

A veces una asociación mixta es necesaria ponerla en modo texto. Para ello se utilizan los símbolos "+" y "//" para designar las asociaciones serie y paralelo respectivamente. Así con (R1 + R2) se indica que R1 y R2 están en serie mientras que con (R1//R2) que están en paralelo. De acuerdo con ello, las asociaciones de la figura 5 se pondrían del siguiente modo:En una asociación mixta podemos encontrarnos conjuntos de resistencias en serie con conjuntos de resistencias en paralelo. En la figura 5 pueden observarse tres ejemplos de asociaciones mixtas con cuatro resistencias.

a) (R1//R2)+(R3//R4)

b) (R1+R3)//(R2+R4)

c) ((R1+R2)//R3)+R4

CIRCUITO INTEGRADO

Un circuito integrado (CI), también conocido como chip o microchip, es una estructura de pequeñas dimensiones de material semiconductor, de algunos milímetros cuadrados de área, sobre la que se fabrican circuitos electrónicos generalmente mediante fotolitografía y que está protegida dentro de un encapsulado de plástico o cerámica. El encapsulado posee conductores metálico sapropiados para hacer conexión entre el CI y un circuito impreso. 

HISTORIA

En abril de 1949, el ingeniero alemán Werner Jacobi¹ (Siemens AG) completa la primera solicitud de patente para circuitos integrados con dispositivos amplificadores de semiconductores. Jacobi realizó una típica aplicación industrial para su patente, la cual no fue registrada.

Más tarde, la integración de circuitos fue conceptualizada por el científico de radares Geoffrey Dummer (1909-2002), que estaba trabajando para la Royal Radar Establishment del Ministerio de Defensa Británico, a finales de la década de 1940 y principios de la década de 1950.

El primer circuito integrado fue desarrollado en 1959 por el ingeniero Jack S. Kilby¹ (1923-2005) pocos meses después de haber sido contratado por la firma Texas Instruments. Se trataba de un dispositivo de germanio que integraba seis transistores en una misma base semiconductora para formar un oscilador de rotación de fase.

En el año 1990 Kilby fue galardonado con el Premio Nobel de Física por la enorme contribución de su invento al desarrollo de la tecnología.²

Robert Noyce desarrolló su propio circuito integrado, que patentó unos seis meses después. Además resolvió algunos problemas prácticos que poseía el circuito de Kilby, como el de la interconexión de todos los componentes; al simplificar la estructura del chip mediante la adición de metal en una capa final y la eliminación de algunas de las conexiones, el circuito integrado se hizo más adecuado para su producción en masa. Además de ser uno de los pioneros del circuito integrado, Robert Noyce también fue uno de los co-fundadores de Intel Corporation, uno de los mayores fabricantes de circuitos integrados del mundo.³

Los circuitos integrados se encuentran en todos los aparatos electrónicos modernos, tales como relojes, automóviles, televisores, reproductores MP3, teléfonos móviles, computadoras, equipos médicos, etc.

El desarrollo de los circuitos integrados fue posible gracias a descubrimientos experimentales que demostraron que los semiconductor, particularmente los transistores, pueden realizar algunas de las funciones de las válvulas de vacío.

La integración de grandes cantidades de diminutos transistores en pequeños chips fue un enorme avance sobre el ensamblaje manual de los tubos de vacío (válvulas) y en la fabricación de circuitos electrónicos utilizando componentes discretos.

La capacidad de producción masiva de circuitos integrados, su confiabilidad y la facilidad de agregarles complejidad, llevó a su estandarización, reemplazando circuitos completos con diseños que utilizaban transistores discretos, y además, llevando rápidamente a la obsolescencia a las válvulas o tubos de vacío.

Son tres las ventajas más importantes que tienen los circuitos integrados sobre los circuitos electrónicos construidos con componentes discretos: su menor costo; su mayor eficiencia energética y su reducido tamaño. El bajo costo es debido a que los CI son fabricados siendo impresos como una sola pieza por fotolitografía a partir de una oblea, generalmente de silicio, permitiendo la producción en cadena de grandes cantidades, con una muy baja tasa de defectos. La elevada eficiencia se debe a que, dada la miniaturización de todos sus componentes, el consumo de energía es considerablemente menor, a iguales condiciones de funcionamiento que un circuito electrónico homólogo fabricado con componentes discretos. Finalmente, el más notable atributo, es su reducido tamaño en relación a los circuitos discretos; para ilustrar esto: un circuito integrado puede contener desde miles hasta varios millones de transistores en unos pocos milímetros cuadrados⁴ .

Los avances que hicieron posible el circuito integrado han sido, fundamentalmente, los desarrollos en la fabricación de dispositivos semiconductores a mediados del siglo XX y los descubrimientos experimentales que mostraron que estos dispositivos podían reemplazar las funciones de las válvulas o tubos de vacío, que se volvieron rápidamente obsoletos al no poder competir con el pequeño tamaño, el consumo de energía moderado, los tiempos de conmutación mínimos, la confiabilidad, la capacidad de producción en masa y la versatilidad de los CI.⁵

Entre los circuitos integrados más complejos y avanzados se encuentran los microprocesadores, que controlan numerosos aparatos, desde teléfonos móviles y hornos a microondas hastacomputadoras. Los chips de memorias digitales son otra familia de circuitos integrados, de importancia crucial para la moderna sociedad de la información. Mientras que el costo de diseñar y desarrollar un circuito integrado complejo es bastante alto, cuando se reparte entre millones de unidades de producción, el costo individual de los CIs por lo general se reduce al mínimo. La eficiencia de los CI es alta debido a que el pequeño tamaño de los chips permite cortas conexiones que posibilitan la utilización de lógica de bajo consumo (como es el caso de CMOS), y con altas velocidades de conmutación.

A medida que transcurren los años, los circuitos integrados van evolucionando: se fabrican en tamaños cada vez más pequeños, con mejores características y prestaciones, mejoran sueficiencia y su eficacia, y se permite así que mayor cantidad de elementos sean empaquetados (integrados) en un mismo chip (véase la ley de Moore). Al tiempo que el tamaño se reduce, otras cualidades también mejoran (el costo y el consumo de energía disminuyen, y a la vez aumenta el rendimiento). Aunque estas ganancias son aparentemente para el usuario final, existe una feroz competencia entre los fabricantes para utilizar geometrías cada vez más delgadas. Este proceso, y lo esperado para los próximos años, está muy bien descrito por la International Technology Roadmap for Semiconductors. ⁶